ミ−散乱ライダー信号の解析手法
杉本伸夫、劉 兆岩*
Data Analysis Methods for Mie-Scattering Lidars
Nobuo Sugimoto and Zhaoyan Liu
国立環境研究所 大気圏環境研究領域 遠隔計測研究室
〒305-0053つくば市小野川16-2
*現在の所属:ハンプトン大学、大気科学センター
National Institute for Environmental Studies
16-2 Onogawa, Tsukuba, Ibaraki 305-0053, Japan
*Present address: Center of Atmospheric Science, Hampton University, 23 Tyler Street, Hampton, VA 23668
Contact person: Nobuo Sugimoto (nsugimot@nies.go.jp)
Abstract
Data analysis method for Mie-scattering lidar observations of the atmosphere are reviewed. Mie scattering lidar method is the simplest lidar method and is widely used in the ground-based observations of clouds and aerosols. Space-borne lidars such as GLAS and ESSP-3 are being developed in the Unites States and planned to be launched in the near future. ESA and NASDA also have a joint program including a space-borne Mie scattering lidar. A Mie-scattering lidar is simple in the hardware system, but there is a difficulty in quantitative data analysis. The lidar equation which describe the lidar signal contains two unknown parameters, namely, backscatter coefficient and extinction coefficient. Therefore the lidar equation cannot be solved without an assumption on the relationship between the two parameters. Various data analysis methods, consequently, have been studied to determine these parameters quantitatively, for various measurement conditions. This paper describes these methods for both ground-based and space-borne lidars.
ミ−散乱ライダー信号の解析手法
目次
1.はじめに
2.ミー散乱ライダーの原理とライダー方程式
3.ライダー信号の解析手法
3−1 Slope法とSlant-path法
3−2 Extinction/backscatter ratio (S-ratio)法
3-2-1 Forwardインバージョン法
3-2-2 2成分(エアロゾルと大気構成分子)を考えたforwardインバージョン法(Fernaldの方法)
3-2-3 Backwardインバージョン法(Klettの方法)
3-2-4 Backwardの2成分のインバージョン法(Fernaldの方法)
3-2-5 Optical-depth-constrain (ODC)のインバージョン法
3-2-6 多重散乱を考慮したインバージョン法
3-3 2波長を用いる解析手法
3-4 Combined S-ratio and slant-path
3-5 多成分を考慮したライダー方程式の解
4.おわりに
1.はじめに
ライダー(レーザーレーダー)は、レーザーを光源とする能動的な遠隔観測手法である。これまでに、大気の各種のパラメータ(エアロゾル、雲、水蒸気、オゾン、大気汚染気体、気温、風向風速など)の測定のためのさまざまなライダーシステムが開発されてきた。その中で、ミー散乱ライダーはエアロゾル、雲を測定する最も簡便なライダー手法で、現在、地上ライダー観測に広く利用されている。また、衛星搭載ミー散乱ライダーによる雲、エアロゾルの全球観測は、地球温暖化などの気候変動の研究や監視に大きな役割を果たすと期待されている。
雲は大気放射収支に、太陽光及び地表からの熱放射の散乱吸収を通じて非常に大きな効果を持つ。またエアロゾルは太陽光を散乱する直接効果と雲の生成の核として働く間接効果を持つ。特に後者は重要であるが十分に解明されておらず、現在の気候変動予測の不確定性の大きな原因と考えられている。そこで雲、エアロゾルの分布と放射特性の全球的観測が必要とされている。
ライダーはエアロゾルの分布および光学特性の最も有効な観測手法のひとつである。特に高度分布が得られることがライダーの最大の特長である。また、対流圏上部の巻雲の観測もライダーに最も期待される観測対象である。一方、雲レーダーなどと組み合わせることによって、雲水量などのパラメータを導出する手法も期待されている。これらの応用ではライダー信号の定量的な解析が不可欠である。
ライダー測定において、レーザー光は雲やエアロゾルおよび大気構成分子に散乱されると同時に、散乱や吸収によって減衰される。そのため、ライダー信号を表すライダー方程式には大気の後方散乱係数と消散係数の2つの未知数が含まれる。従って、厳密な意味ではライダー方程式は解けない。そこで、これまでに様々な解析手法が提案されてきた。本文では、これらの手法をレビューするとともに、筆者らによるシミュレーションの結果も交えて、それぞれの解析手法の応用範囲や問題点などについて議論する。
2.ミー散乱ライダーの原理とライダー方程式
ミー散乱ライダーはパルスレーザー光を大気中へ発射し、大気中のエアロゾルや分子による後方散乱光を時間の関数として記録する。レーザーを送信した時間から信号を受信するまでの時間遅れからレーザーが散乱された距離が求められ、受信光強度からレーザーの光路に沿った散乱強度の分布が得られる。Fig. 1に一般的なミー散乱ライダーの構成を示す。
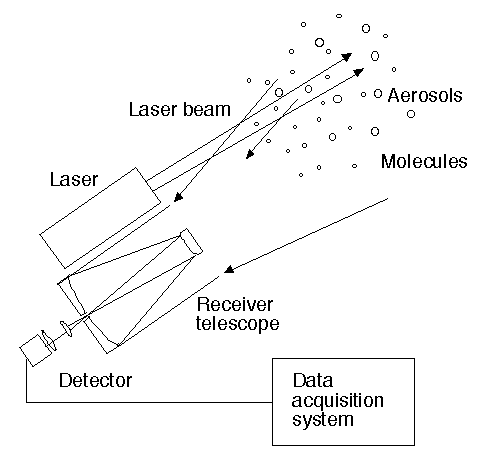
Fig. 1 Concept of Mie scattering lidar method
ライダー信号を表すライダー方程式は次式で表される。
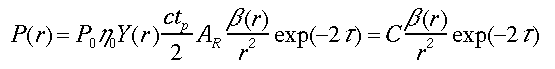 (1)
(1)
ここで、P(r)は受信信号強度、r は計測距離、P0は送信レーザーのパワー、η0はライダーシステムの光学的な効率である。Y(r) はライダーの送受信系の重なりを現す関数である。Y(r)はある距離から1となるような関数である。そこで、以下の取扱では、Y(r) = 1とする。ctpは送信レーザーパルスの空間的な長さ、AR は受信望遠鏡の有効受信面積、β(r)は距離rでの大気の体積後方散乱係数。C=P0η0ctpAR/2は距離に依存しないライダー定数である。
τは大気の光学的厚さで次式で表される。
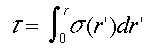 (2)
(2)
ここで、 σ(r)は大気の散乱と吸収による減衰を表す消散係数である。
ライダー信号の解析は、式(1)のライダー方程式を解いて後方散乱係数β(r)、消散係数σ(r)を求めることに他ならない。数学的な観点からは、1つのライダー方程式から後方散乱係数と消散係数の2つのパラメータを決めることはできない。そこで、測定状況等に応じて、近似や仮定をおいてライダー方程式を解くことになる。次節以降では、様々なライダー方程式の解法について考察する。
3.ライダー信号の解析手法へ
目次に戻る

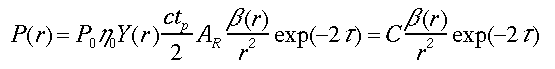 (1)
(1)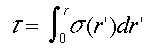 (2)
(2)