ミ−散乱ライダー信号の解析手法
3-2-4 Backwardの2成分のインバージョン法(Fernaldの方法)
レイリー散乱の無視できない場合について、Fernaldは2成分のbackwardのインバージョン法を提案した31)。現在、2成分のインバージョン法はforwardとbackwardともにFernaldの方法と呼ばれる。Klettもその後2成分のライダー方程式を研究し、Fernaldの方法では定数と仮定されていた S パラメータを距離の関数に拡張した12)。2成分法はエアロゾルや雲の散乱の無視できる高度において、大気構成分子のレイリー散乱を利用して境界条件を与えられるという大きな利点を持つ。S1を定数とする2成分の解は次の2つの式で表される。
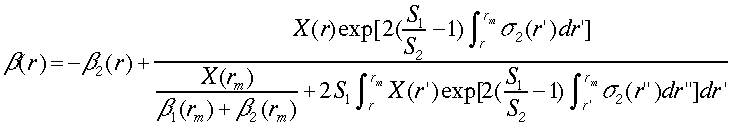 (22)
(22)
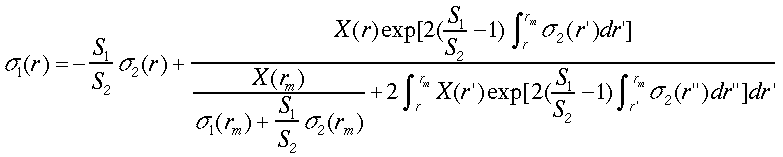 (23)
(23)
2成分のbackwardインバージョン法は1成分の場合と同様の収束特性を持ち、安定である。2成分のインバージョンの境界値の誤差に対する感度は次式で表わされる。
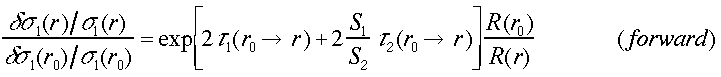 (24)
(24)
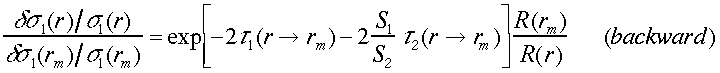 (25)
(25)
ここで、τ1とτ2 はそれぞれミー散乱とレイリー散乱による光学的厚さ、R=β1 /(β1+β2 )は後方散乱係数比である。2成分のインバージョンが、1成分と同様の発散(forward)、収束(backward)の特性を持つことが分かる。ミ−散乱の小さい(Rの十分に小さい)大気の散乱信号より、境界条件を決める場合、σ1=0(|dσ1/σ|=1)であるが、R(r0) あるいは R(rm)は十分に小さいため境界条件の誤差は小さい。
2成分の場合backward、forwardともにS1パラメータが必要である。Fig. 4にS1に含まれる誤差の影響を示す筆者らのシミュレーション結果を示す。ここで、標準大気のレイリー散乱と地面から1.5kmの高度に均一に分布するエアロゾル層のミ−散乱の2成分から成るモデルを考えた。エアロゾルのS1の真値を50 srと仮定した。エアロゾル層の上の1.5 km以上のレイリー散乱信号により境界条件を与え、S1 =30、70 srとしてインバージョンを行った。IBCと光学的厚さの算出値とモデル値の比をFig. 4に 示す。
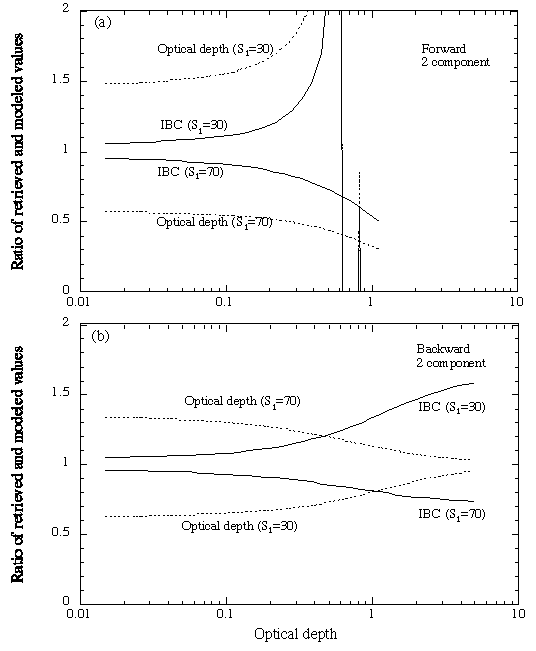
Fig. 4 Ratios of retrieved and modeled values of IBCs and optical depths for the 2-component forward and backward inversions simulated with a two-component model consisting of a homogeneous aerosol layer with a thickness of 1.5 km and the US standard atmosphere.
Fig. 4(b)より、backwardの場合、IBC(あるいは後方散乱係数)の誤差は光学的厚さとともに大きくなり、光学的厚さ(消散係数)の誤差は小さくなる。光学的厚さが小さい場合IBCの誤差は小さくなるが、S1の誤差の影響はゼロにはならず一定の比率で誤差が残ることに注意が必要である。一方、forwardの場合は、Fig. 4(a)のように消散係数、後方散乱係数ともに、誤差が光学的厚さとともに増加する。また、消散係数の誤差は後方散乱係数の誤差より大きい。
2成分のライダー信号の解析法は、境界層や対流圏のエアロゾル、成層圏エアロゾル、光学的に薄い巻雲などのデータ解析に用いられる。これらの場合光学的厚さは比較的小さいので、forward、backwardともに利用できる。いずれを用いるかは、境界条件の与えやすさによって決められる。ミー散乱が大きい場合には、レイリー散乱はミー散乱に対して小さくなるので、2成分の式(16)、(17)、(22)と(23)はそれぞれ1成分の式(10)、(11)、(18)と(19)となる。すなわち、1成分の解は、2成分の解の1つの特殊な場合である。
3-2-5 Optical-depth-constrain (ODC)のインバージョン法へ
3-2-4 Backwardの2成分のインバージョン法(Fernaldの方法)の先頭へ戻る
目次に戻る
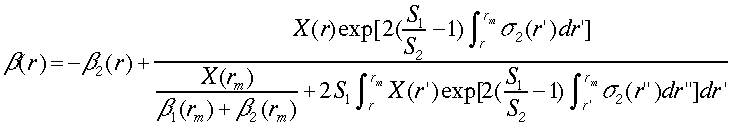 (22)
(22)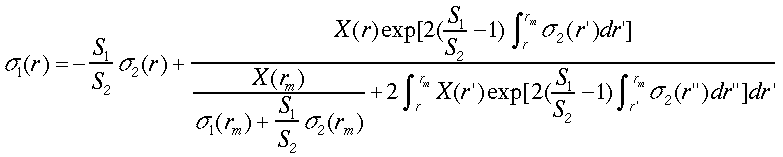 (23)
(23)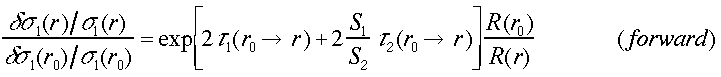 (24)
(24)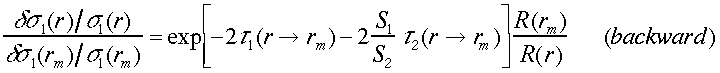 (25)
(25)