ミ−散乱ライダー信号の解析手法
3-2-5 Optical-depth-constrain (ODC)のインバージョン法
Davisは、雲の透過率(光学的厚さ)が求められる場合のデータ解析法を検討し、1成分の解法に基づくイタレージョンによってSパラメータと消散係数(後方散乱係数)を同時に求める手法を示した7)。また、Fernaldらは、1成分の場合、イタレージョンを行うことなくS パラメータを求める解析式を示した13)。その後、光学的厚さを拘束条件とする(ODC)解が求められた32, 33)。Sを定数とし、r0とrmの間の大気の光学的厚さをtauとすると式(1)と(18)から、
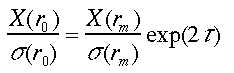 (26)
(26)
と
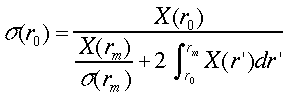 (27)
(27)
が得られる。式(26)、(27)から、次式が求められる。
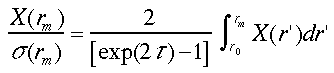 (28)
(28)
この関係を式(18)に代入すれば1成分のODCの解、(29)式が得られる32, 33)。
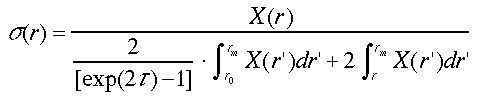 (29)
(29)
r0 と rmの間の光学的厚さあるいは透過率T=exp(-τ)が推定できれば、(29)式で消散係数のプロファイルが得られる。透過率は、エアロゾル層の上下のレイリー散乱信号、やsun-photometerなどの他の測定によって求める7, 13, 33)。式(29)は、光学的に厚い場合も発散することがなく安定である。
ここで、感度解析により、この解の安定性や精度を考察する。光学的厚さの誤差に対する感度は次式で表される。
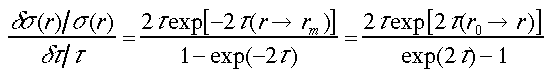 (30)
(30)
(30)式と、(20)と(21)より、1成分のODC解とforward、backwardの解を比較する。2τ/[1-exp(-2τ)]>1と2τ/[exp(2τ)-1]<1の関係があるので、
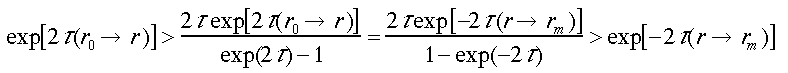 (31)
(31)
である。すなわち、ODCの誤差感度はforwardより小さく、backwardより大きい。例として、厚さ1kmの均一に分布する散乱体に対してODC、forwardとbackwardの境界値の誤差に対する感度を計算した結果をFig. 5に示す。光学的厚さ0.05の小さい場合、感度はいずれもほぼ同じであるが、光学的厚さが1と5の場合は感度は大きく異なる。また、感度は forwardの場合は1より大きく(誤差の増幅)、backwardの場合は1より小さい(誤差の減衰)。一方、ODCの誤差係数は手前では1より小さく遠方で1より大きい。
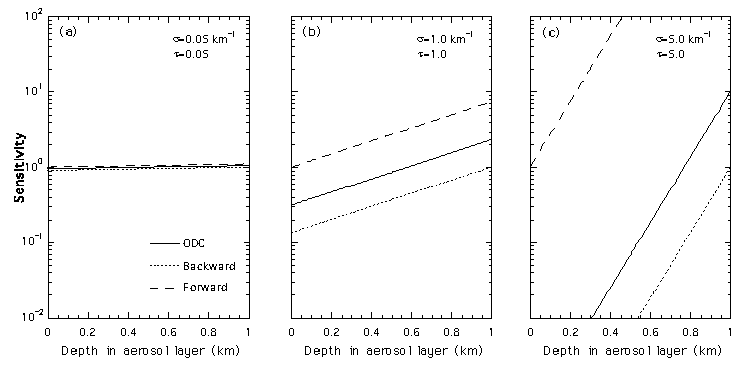
Fig. 5 Comparion of sensitivities for the ODC, forward and backward inversions to the boundary condition variations.
(29)式のODCの解は、forward、backwardの解のように境界での信号X(r0 )或いはX(rm)(式(10)と(16)の分母の第1項)に含まれる雑音の影響を受けることがない。その結果、境界での信号の雑音が大きい場合には、ODCのインバージョンの方が backwardより良いことも示されている34)。
式(8)を式(29)に代入すると、後方散乱係数に対するODC解も求められ、次式で表される。
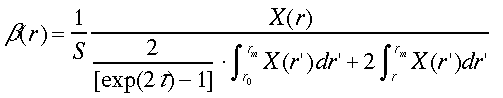 (32)
(32)
手前(遠方)においた境界における後方散乱係数β(r0 )(β(rm ))が分れば、あるいはライダー定数Cと散乱体までの透過率T(r0)が推定ができれば、Sパラメータ推定もできる。r=r0 (あるいはr=rm )を式(32)に代入すれば、次の式が求められる。
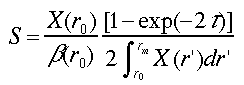 (33a)
(33a)
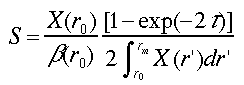 (33b)
(33b)
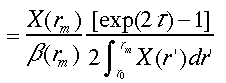 (33c)
(33c)
ここで、式(12)の関係を利用した。式(33a)、(33b)はFernaldらの求めたSの解析式と等価である。Sの誤差の境界条件、光学的厚さの推定誤差に対する依存関係を求めると次のように表わされる。
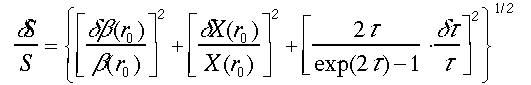 (34a)
(34a)
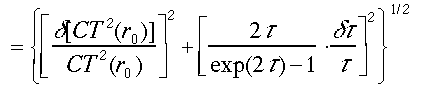 (34b)
(34b)
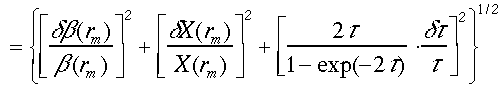 (34c)
(34c)
ここで、3つの式の右辺の第1項は境界条件の推定誤差、最後の項は光学的厚さの推定誤差の寄与である。式(34a)、(34b)、(34c)より、境界条件の推定誤差と境界での信号雑音あるいはCT2(r0)の推定誤差が直接にSの推定に影響する。一方、光学的厚さの推定誤差dt/τ の寄与は光学的厚さに依存する。式(33a)、(33b)では、光学的厚さが大きい場合に誤差が減衰され、一方、式(33c)では誤差が増幅される。
式(33)によりSが推定されれば、式(32)より後方散乱係数が求められる。後方散乱係数の算出では式(34)を通じて境界条件の誤差の影響を受ける。
レーザー光が雲を透過することができない場合(T2=exp(-2τ→0)、式(33)は
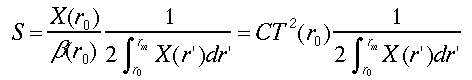 (35)
(35)
となる。すなわち、光学的に厚い雲の場合、手前の境界値あるいは CT2(r0) が分かれば、S パラメータの推定ができる。しかし、実際の観測では、光学的に厚い雲の散乱信号には多重散乱成分が含まれ、それを考える必要がある。多重散乱を考えたインバージョン法については次節で述べる。
Fernaldらは13)、2成分の場合にもエアロゾル層の透過率(光学的厚さ)が求められれば、消散係数と後方散乱係数の比S1が求められることを指摘した。1成分と同様に、光学的厚さを拘束条件とする(ODC)2成分のライダー方程式の解が得られ、次式で表される33)。
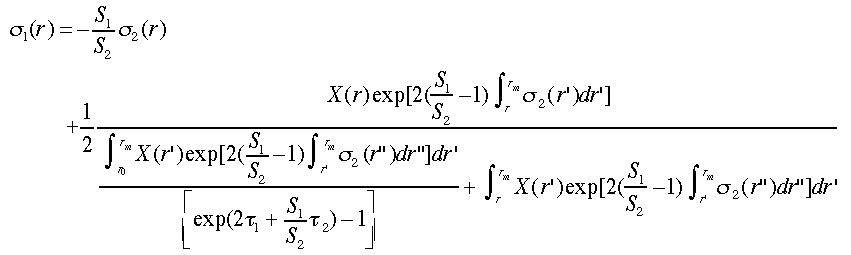 (36)
(36)
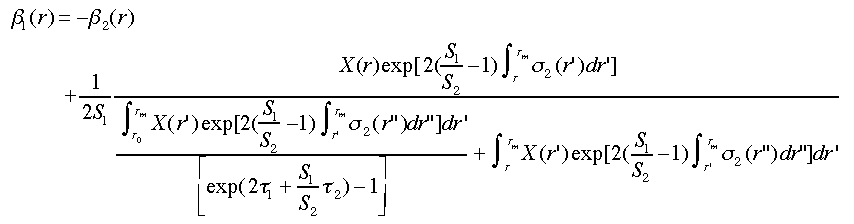 (37)
(37)
ここで、τ1とτ2はそれぞれ、r0とrmの間のエアロゾルや雲による光学的厚さと分子による光学的厚さである。2成分のforwardやbackwardのインバージョン法と同様に、2成分のODC解ではS1パラメータが要求される。しかし、境界条件が推定ができれば、次式でS1も求められる。
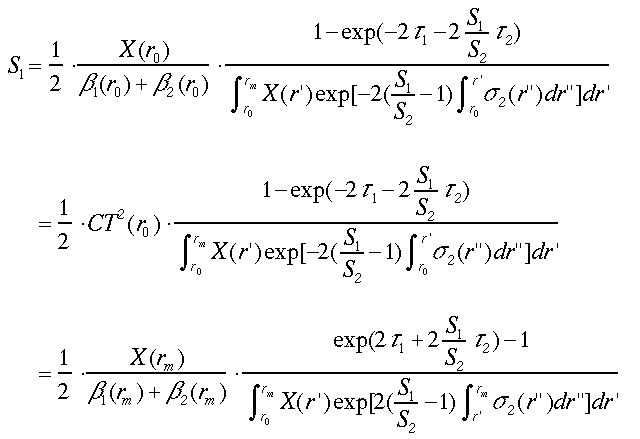 (38)
(38)
式(38)には解析解がなく、次に述べるイタレーションによりS1を求める必要がある。適当な値(例えば0)をS1の初期値として、式(38)の右側に代入しS1を計算する。算出されたS1を再びに式(38)の右側に代入しS1を計算する。このように反復してS1の計算を行ない、新たに算出されたS1と前回の値との差が一定の値以下になったら、反復を中止して最後の値をS1の解とする。
2成分の消散係数のODCの解(36)式も、S1を求める(38)式も、境界における信号X(r0 )あるいはX(rm )を含み、1成分のODCの解(29)式のように境界での信号雑音の影響を受けないという利点はない。
レイリー散乱がミー散乱と比べて小さく無視できる場合、2成分の式(36)、(37)、(38)は1成分の式(29)、(32)、(33)となる。
3-2-6 多重散乱を考慮したインバージョン法へ
3-2-5 Optical-depth-constrain (ODC)のインバージョン法の先頭へ戻る
目次に戻る
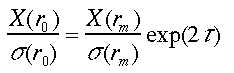 (26)
(26)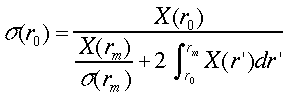 (27)
(27) 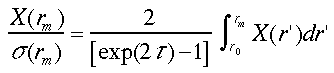 (28)
(28)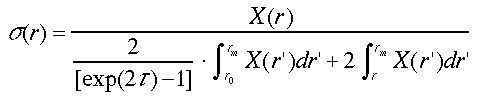 (29)
(29)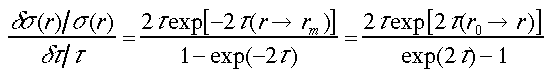 (30)
(30)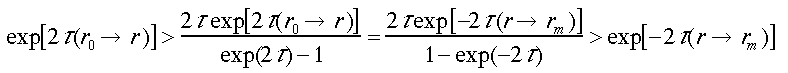 (31)
(31)
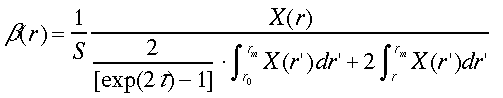 (32)
(32)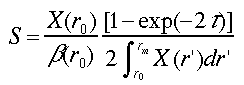 (33a)
(33a)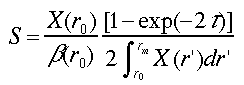 (33b)
(33b)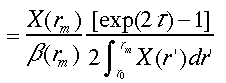 (33c)
(33c)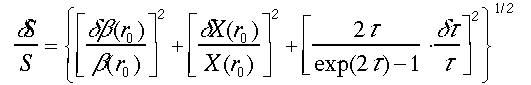 (34a)
(34a) 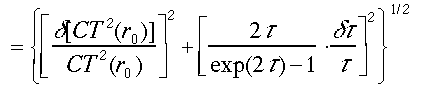 (34b)
(34b) 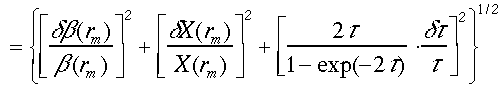 (34c)
(34c) 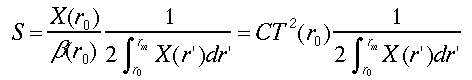 (35)
(35)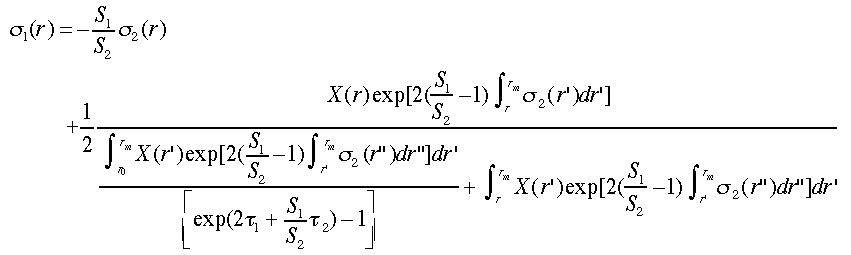 (36)
(36)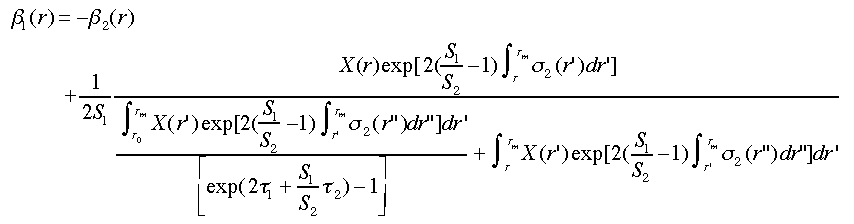 (37)
(37)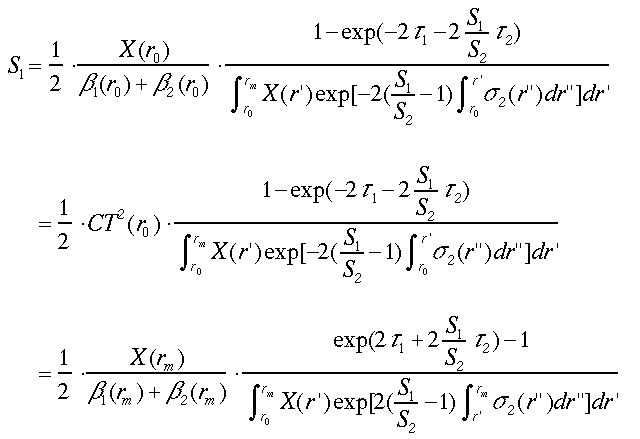 (38)
(38)