ミ−散乱ライダー信号の解析手法
3-3 2波長を用いる解析手法
これまでに述べた解析手法は、1波長のライダーの解析のために開発されたものであるが、2波長のライダーデータを用いてエアロゾルの散乱パラメータを求める解析法も開発された。Sasano-Browellは52)、2波長のデータからエアロゾルの消散係数・後方散乱係数比S1を求められる方法を提案した。この方法では、エアロゾルの粒径分布や屈折率は一様で濃度のみに分布があると考え、異なる波長から求めたエアロゾルのプロファイルが相似になることを仮定する。
Liuらは、相似の度合いの評価関数を次式で定義した53)。
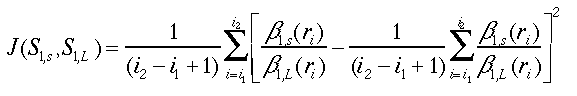 (53)
(53)
ここで、添字のsとLは短波長、長波長を表わす。i1とi2はエアロゾル層の中の2つの距離で、この距離区間の後方散乱係数を用いて評価関数 J を計算する。この評価関数は、Sasano-Browell52)が用いたものと異なり、2波長の後方散乱係数の比の標準偏差を用いている。後方散乱係数が相似の場合、2波長の後方散乱係数の比が定数であるため、この比の標準偏差は0となる。すなわち、S1と境界条件が真値に近いならば、後方散乱係数は2波長で正しく求められ、評価関数J が最小となる(雑音が無ければ0となる)。境界値が正しく与えられる場合、S1を変えてJを計算して最小となるS1を探せば、S1を決めることもできる。
2波長法では、エアロゾルの後方散乱係数を求めるために2成分の解、 (16) 式または(22) 式を用いて。また、エアロゾルのS1の値は通常、0と90 sr の範囲にあるので、長波長の消散係数対後方散乱係数比S1,Lの2つの限界の値として0と90を与え、これに応じて、短波長の消散係数・後方散乱係数比S1,sの2つの値を求めることができる。具体的には、まず、S1,L=0、90に対して、長波長の2つの後方散乱プロファイルを求めこれらを参照プロファイルとする。次に、評価関数を用いて、2つの参照プロファイルに最も近い2つの短波長の後方散乱プロファイルを見つける。これによってS1,sの2つの限界を決める。現実のS1,sは求めた2つの限界の間にある。また、後方散乱係数プロファイルが2つの参照プロファイルの間にある。このように求めたS1,sの範囲は、エアロゾルの光学的厚さが小さいときに小さいことが示されている52-53)。
光学的厚さの大きいときは、長波長と短波長のインバージョンともにS1に敏感であるので、もしS1,LとS1,sを変えて評価関数Jの最小を探せば、S1,LとS1,sを両方とも決められる可能性がある。そこで、Liuらは53)、S1,LとS1,sの両方を求められるように2波長法を拡張した。しかし、2波長法は雑音に敏感であることも示され、応用は雑音の少ないデータに限られる。また、実際には異なる性質のエアロゾルが層状に分布する場合も多く、一様なエアロゾルを仮定した相似の条件は必ずしも現実的ではない。
Potterも、1成分と2成分のライダー方程式の解に基づき2波長のアルゴリズムを提案した54)。この方法も、同様の散乱プロファイルの類似性の仮定を用いる。最近、モデル計算でこの方法が評価され、光学的厚さの小さいときはSが距離に依存して変わっても、インバージョンがSに敏感でないため散乱プロファイルはよく求められることが示された55)。しかし、この方法が雑音に敏感であることも示されている。
3-4 Combined S-ratio and slant-path 法
3-1節に述べたslant-path法は、水平に大気が一様に分布することを仮定し、異なる天頂角のライダー測定より大気の透過率や光学的厚さを求めるものであった。slant-path法を拡張し、消散係数と後方散乱係数の関係を用いれば、エアロゾルのSパラメータ、消散係数と後方散乱係数の導出が可能となる56)。天頂角をq、鉛直高度をzとすると、
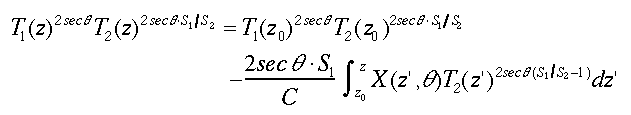 (54)
(54)
が求められる。ここで、T1 (z)とT2 (z)はライダーからzまでのエアロゾルと分子の鉛直方向の透過率である。S1パラメータは定数と仮定されている。分子の透過率は大気の気温、気圧データから求められる。ライダー定数Cは反射率の知られたターゲットなどにより決められる57)。従って、決めなければならない未知数は、エアロゾルのS1パラメータと透過率T1 (z)の2つでなる。エアロゾル分布が水平方向に一様と仮定しているので、異なる天頂角のプロファイルから求めた高度 zにおける透過率は同じはずである。そこで、そのように整合するようにS1パラメータを決める。
この方法によって、単波長のライダーでエアロゾルのS1 、消散係数、後方散乱係数と透過率を求めることが可能であるが、天頂角を変えたライダー測定が必要なこと、また、水平方向のエアロゾル分布が一様である条件が必要なことが応用上の制限となる。
3-5 多成分を考慮したライダー方程式の解
巻雲の解析において、例えば火山の噴火後などは境界条件を与える際にエアロゾル散乱を無視できない58)。また、薄い雲の場合、雲の中のエアロゾル散乱を無視できない。そこで、雲、エアロゾル、分子の3成分を考慮した解析手法が検討されている59)。
4 おわりに
本文では、ミー散乱ライダーの解析手法、すなわち、ライダー方程式に基づいたライダー信号のインバージョン法についてレビューを行った。また、感度解析やシミュレーション評価を交えてこれらの方法の比較を行った。
消散係数と後方散乱係数の間に関係を仮定するextinction/backscatter ratio(S-ratio)法による、forward、backward、optical-depth-constrain(ODC)のインバージョン法は多くの条件に適用できる。一般に、backwardインバージョン法による解は安定で、特に光学的に濃い測定対象の解析に有用である。forwardのインバージョン法は濃い測定対象では不安定である。一方、 ODCのインバージョン法は、forward法のように濃い測定対象でも発散することがなく安定する。
2波長法とS-ratio and slant-path combinedの法は、境界層エアロゾルなどの解析に利用できる。これによって、エアロゾルのSパラメータの推定もできる。しかし、エアロゾルの散乱プロファイルの相似性や水平方向の均一性などの仮定はこれらの方法の応用を制限する。また、2波長法は測定の雑音に敏感である。
衛星ライダーや視野角の大きいライダーでは多重散乱の効果が重要である。多重散乱の効果は多重散乱因子を用いて近似的にライダー方程式に取り込むことができる。多重散乱因子はシミュレーション等によってあらかじめ推定する必要がある。
1波長のミ−散乱ライダーでは、ODCや、slant-path法など特別な条件が得られる場合を除いて消散係数・後方散乱係数比(ライダー比)S1 を仮定することが必要である。エアロゾルのライダー比は複素屈折率、粒径分布、形状、測定波長に依存する。
水雲のS1は波長に大きく依存せず一定値が仮定できるが、氷雲のS1は粒子形状に大きく依存する。
ミ−散乱ライダーの応用においては、ライダー比の気候値がエアロゾルのタイプ毎に得られていることが重要である。ライダー比は高スペクトル分解ライダーやラマンライダーによって測定が可能である。また、観測上の制約はあるが、ミ−散乱ライダーと放射計を組み合わせることでS1を決めることもできる。今後、これらの手法による気候学的な研究が必要である。一方、雲については、雲レーダーと組み合わせた解析が期待される60, 61)。
筆者らは、NASDAのELISE を想定して、本文で述べた各種のデータ解析手法の検討を行ってきた53) 。残念ながらELISEの計画は中止されたが、NASAのGLASが2002年に、同じくESSP-3 (PICASSO) が2004年に打ち上げられる計画である。これらの衛星ライダーを利用した雲、エアロゾルの立体分布の全球的観測がいよいよ現実のものとなる。また、これらのデータと地上観測を組み合わせた利用研究が期待される。さらに、NASDAと欧州宇宙機構の協力による地球放射ミッションEarthCAREが提案されている。その中では、ライダーと雲レーダーを同じ衛星に搭載することが計画され、さらに高度なデータ解析手法の開発が必要とされている。
目次に戻る
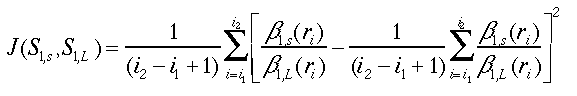 (53)
(53) 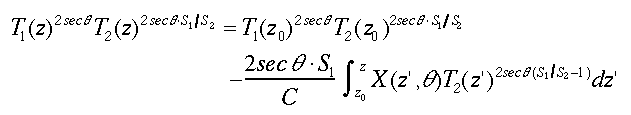 (54)
(54)