ミ−散乱ライダー信号の解析手法
3-2-3 Backwardインバージョン法(Klettの方法)
前述のforwardインバージョン法は、光学的厚さが約2以上の大きい場合には不安定で、光学的に厚い散乱体の解析には適用できない5-6)。その原因は、ライダー方程式の解、式(10)と(11)(1成分の場合)及び(16)と(17)(2成分の場合)の分母の積分項の符号が負であることによる。
Klettは、安定な1成分のbackwardインバージョン法を提案した24)。これは、現在、Klettの方法として知られる。この方法では、境界条件を遠方に置いて手前に積分する。遠方の境界値 X(rm)、σ(rm)とβ(rm)をそれぞれ式(10)と(11)に代入すると、消散係数と後方散乱係数に対する解が得られ、それぞれ次式で表される。
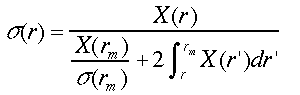 (18)
(18)
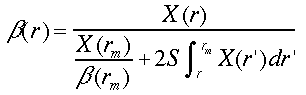 (19)
(19)
(18)、(19) 式では、分母にある積分項の符号が正であるので、積分を進めるとともに分母が増大し境界値の誤差や雑音の影響が小さくなる。従って、解は安定である。Klettは、数値計算によりforwardとbackwardのインバージョンの安定性の違いを示した24)。
Fig.2に光学的に厚い散乱体について、Klettのシミュレーションを再現した例を示す。実線は与えたモデルの消散係数の分布、破線は求めた消散係数の分布である。また、消散係数の境界値、σ(r0)とσ(rm)、にそれぞれ±1%と±50%の誤差を与えた。境界値にわずか1%の誤差を与えたforwardインバージョンは発散するが、一方、50%の誤差を与えてもbackwardではよく収束する。
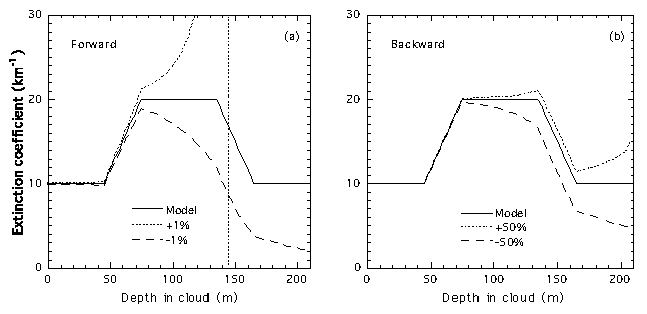
Fig. 2 Inversion simulation for a modeled dense cloud using solutions of the 1-component lidar equation, Eqs (10) and (18), showing the different stabilities of forward and backward inversions.
このようにbackwardインバージョン法は境界値の誤差が大きくても収束するので、消散係数の境界値をスロープ法などで推定することができる。Klettは境界条件の与え方についても議論している24)。インバージョンの誤差についてはこれまでに多くの研究が行われ、境界値の誤差、信号の誤差、消散係数・後方散乱係数比Sの誤差などの影響が調べられている12, 24-30)。
Bissonnetteは、インバージョンの誤差の解析式を求め、数値計算と同様、backwardインバージョンは収束し、forwardでは発散する特性を示した30)。ここで、例をとして消散係数の境界値の誤差がforwardとbackwardのインバージョンにどのように影響するかを考察する。インバージョンで求めた消散係数の誤差の境界値の誤差に対する感度は、次の式で表される。
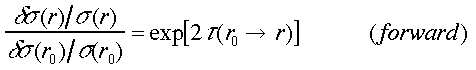 (20)
(20)
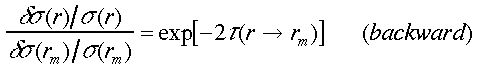 (21)
(21)
式中、τ(r0→r)とτ(r→rm)はそれぞれr0→rとr→rmの間の光学的厚さを表す。これらの式から、境界条件の誤差は、forward の場合、積分の距離とともに指数関係的に増幅され、backwardの場合は低減されることがわかる。また、以下のことがいえる。
1)巻雲などの薄い散乱体に対しては、forwardとbackwardの誤差感度が大きく違わないので両方の方法が使える。例えば、光学的厚さτ = 0.05、0.5、5.0に対して、境界値の誤差に対する誤差感度はforwardの場合、約 1.1、2.7、22000、backwardの場合、約 0.9、0.37、0.00005である。光学的厚さが 0.05 の場合、forwardとbackwardの誤差感度の比はわずか約 1.2 である。光学的厚さが 0.5 の場合はこの比は約 7.4 と大きいが、もし手前の境界条件が遠方の 7.4 倍以上の精度で決められる状況ならばforwardが有効な場合もある。
2)積雲などのような光学的に濃い散乱体に対しては、forwardインバージョンは不安定である。境界条件にわずかな誤差があれば遠方で非常に大きな誤差が生じる。また、信号に含まれる雑音にも敏感である。一方、backwardの場合は、近距離で消散係数は真値に収束する。例えば、τ = 5.0 の場合、境界値に真値の約50倍の大きな誤差があっても、手前での誤差は0.01 % である。従って、光学的に厚い散乱体ではbackwardインバージョン法を用いる必要がある。
後方散乱係数に対しても、 (20)、(21) 式と同様な関係が得られ、境界条件の誤差の影響は同様である。しかし、後方散乱係数の導出では S パラメータが必要であるので、S に含まれる誤差の影響を考慮する必要がある。Fig.3に、厚さ1.5 km、均一分布のエアロゾルに対する筆者らのシミュレーション結果を示す。まず、エアロゾルの消散係数(光学的厚さ)を変えてライダー信号を作り、式(11)と(19)によりインバージョンを行った。ここで、Sのモデル値(真値)は50であり、インバージョンでは30と70を与えた。境界条件の誤差は無いものとした。求めたIBC(integrated backscatter coefficient)とIBCの真値の比をFig.3に示す。この比が1から離れるほど誤差が大きいことを意味する。
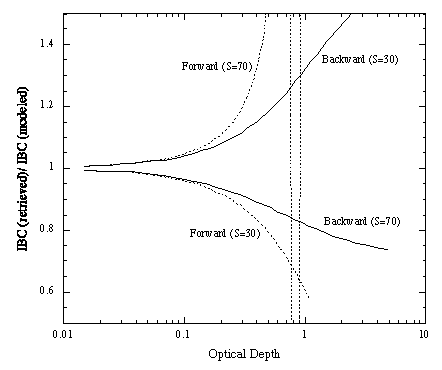
Fig. 3 Ratio of retrieved and modeled integrated-backscatter-coefficient (IBC) as a function of optical depth, showing effects of extinction to backscatter ratio (lidar ratio) on the 1-component forward and backward inversions. A homogeneously distributed aerosol model with a thickness of 1.5 km was assumed and exact boundary values were used in the inversion simulation. A low dependence of the retrieved IBC on the used lidar ratio is shown for both forward and backward in versions for smaller optical depth; a higher lidar ratio dependence can be seen for the forward inversion than the backward invsion for larger optical depth.
Fig.3より、光学的厚さが0.1より小さいときは、Sの相対誤差が±40%と大きくてもIBCの相対誤差は±5%以下と小さいことが分かる。一方、光学的厚さが大きい場合は、誤差が大きい。これは、Sが (11)、(19) 式の分母の積分項(減衰補正項)にあることによる。また、Sを真値より大きく与えると、forwardの場合は後方散乱係数が過大評価され、backwardの場合は逆に後方散乱係数が過小評価される。
3-2-4 Backwardの2成分のインバージョン法(Fernaldの方法)へ
3-2-3 Backwardインバージョン法(Klettの方法)の先頭へ戻る
目次に戻る
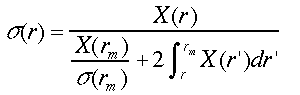 (18)
(18)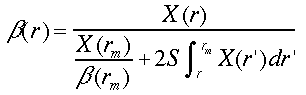 (19)
(19)
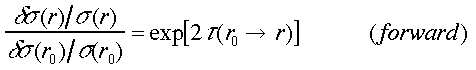 (20)
(20)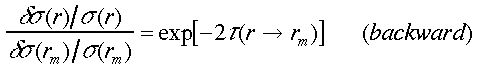 (21)
(21)