図5-1
ここでは、正二十面体をひとつの頂点の周りの5つの面の色が全て異なるように5色で塗り分けることを考えてみました。塗り方はたぶん4通り(?)あります(図5-1)。
図5-1
ところで、このようにして5色に塗り分けた正二十面体の同じ色の面の数は20/5で4面ありますが、この4面を延ばせば正四面体の面となることがわかります。これまでの話のなかで、面と頂点との関係で正二十面体と正十二面体が親戚であること、また正六面体と正八面体が親戚であることを述べました。さて、ここでの正二十面体と正四面体の関係はちょうど正八面体の4面が正四面体の面であるのとちょうど同じ様な関係であると言えます。正二十面体の面のうち、正四面体を構成する同じ色の4つ面の反対側にもこれと平行な面がそれぞれありますが、これも同じ色に塗りかえたとすると、これらは正八面体の面となることがわかります。いずれにしても、正二十面体系と正八面体系の間にも関係があったわけです。
このことは、正十二面体で、もっと明快に見ることができます。図5-2のように、正十二面体の隣り合う正五角形にうまく対角線を引くと互いに直行することがわかります。このようにして、正十二面体の中に正六面体(立方体)を見つけることができます。
図5-2
対称性のある図案はエッシャーの作品が有名ですが、このような図案は案外簡単に作ることができます。まず、書きたい対称性の格子を書きます。つぎにこの格子に突起とか波とか凸凹とかを適当に付けてゆきます。このとき、突起を付けたとするとちょうど対称な場所に正確に窪みを付けることを忘れないように。このようにして、対象性を保ったまま格子を変形していきます。このときは、何を書こうなとどと考えないで、逆に変形された格子が何に見えるかを考えます。すぐに似た形のものを思いつかないときはしばらく置いておいて気が向いたときにまた考えます。さて、筆者の考案した図案を紹介します。これは、正三角形を面とする正多面体の面を隙間なく埋めることができるような図案です。図5-3は正二十面体の展開図の一部ですが、5色で塗り分けてあります。
図5-3
上の図案を、正二十面体に貼ったものを図5-4に示します。この例では3色で塗ってあります。
図5-4
さて、ここで少しリラックスして折り紙で多面体を作るという話をします。これは、折り紙の本にはたぶん「くす玉」として載っていると思いますが、なかなか面白いので紹介します。図6-1のようにして折った要素を多数組み合わせて多面体を作ります。
図6-1
この場合、多面体のひとつの面に相当する三角錐は3つの要素から構成され、ひとつの要素はふたつの面に寄与します。例えば、正4面体を作ろうとすると要素は4×3/2=6個必要です。(実際に正4面体を作ってみると正三角形の面が直角三角錐になるので、この場合は正六面体になってしまいます。)同様にして、面が三角錐でできた「正八面体」を12の要素から、「正二十面体」を30の要素から作ることができます。写真16は30の要素からなる正二十面体の「くす玉」です。
写真16
さらに、正十二面体の正五角形を五つの正三角形で作る、3×5×12/2=90の要素でできる形とか、正二十面体のひとつの正三角形を9つの正三角形で構成する3×9×20/2=270の要素でできる形など、いろいろな形を作ることができます。写真17は270の要素からなる「くす玉」です。
写真17
折り紙で「正二十面体」を作るとき何色かの要素で色分けするのも面白いので試してみてください。3色あるいは5色の要素できれいに色分けができます。赤、青、白でフランスとか、赤、緑、白でイタリア、赤、黄、黒でドイツなどというのも楽しいのではないでしょうか。
ところで、折り紙で「正二十面体」を作るとき三角錐の突起を作る変わりに、内側から要素を組み合わせて、それぞれの面に三角錐の窪みを作ることもできます。これはたぶん折り紙の本には載っていないと思います。内側から要素を組み合わせるので最後のところでやや高度な技術を要しますがやってみれば何とかなります。また、色分けの方法も裏から組み合わせたものの方が対象性が良くわかります。特に5色の要素で色分けしたものは、同じ色の辺が6つずつあってそれらに接する面を考えると正六面体が見えてきます。といっても、こうなるともう実物を手にとって説明しなければわかっていただけないかもしれません。写真18に例を示します。
写真18
直角三角錐は3つの平面が互いに直角に組み合わさったもので、これをもし鏡面で作ると大変面白い光学的な性質を持ちます。これは、コーナーキューブリフレクタとかレトロリフレクタ(逆反射器)とか呼ばれ、これに入射した光は必ず反対の方向に反射されます。銀紙で裏から組み合わせた「正二十面体」を作ると20の要素を持つレトロリフレクタのアレイ(配列)を作ることができます。写真19に。いくつかの折り紙「レトロリフレクタアレイ」を示します。(参考「レトロの条件」)
写真19
写真20
これは、3本の針金で作った正20面体。
写真21
テニスボールや野球のボールが、丁度6面体の3つのつながった面を一枚の皮で作ってそれを2枚を縫い合わせて膨らませた形をしているように、正十二面体のつながった6つの面をそれぞれ帯状の皮としてボールを作ってみました。
2枚の皮の形はこういう感じです。
写真22
これも、同様で、正十二面体ベースの野球ボールです。
同様の正12面体ベースのドームを中国、昆明の世界園芸博覧会でも見つけました。
先日(2001年1月)、デンバーの空港でZomeという面白い教育玩具を見つけて、衝動買いしました。これは、継ぎ手のところの構造が良くできていて、正多面体を全て作ることができます。写真は、正十二面体の中に立方体と正二十面体を作ったものです。Zometool, Inc. (www.zomesystem.com)は、デンバーにある会社のようです。
Hobermanという会社のSphere、Mini Sphereという玩具があります。実は、私は、Hobermanのオリジナルな物を知らなくて、パンダで有名な中国の四川省成都の動物園でMini sphereの模造品を見て買ってしまったのが先でした。下の写真も模造品のものですが、これは八面体ベースの球に近い多面体(4.3節の写真15と同じ形)の頂点をマジックハンドでつないで大きさが変わるようにしたものです。
これの設計がどうなっているか考えてみましょう。下の図(上)のように頂点(外の頂点、中の頂点)が2段のマッジックハンドで結ばれています。外の頂点、中の頂点はそれぞれ、多面体の中心を通る放射状の線上を移動します。
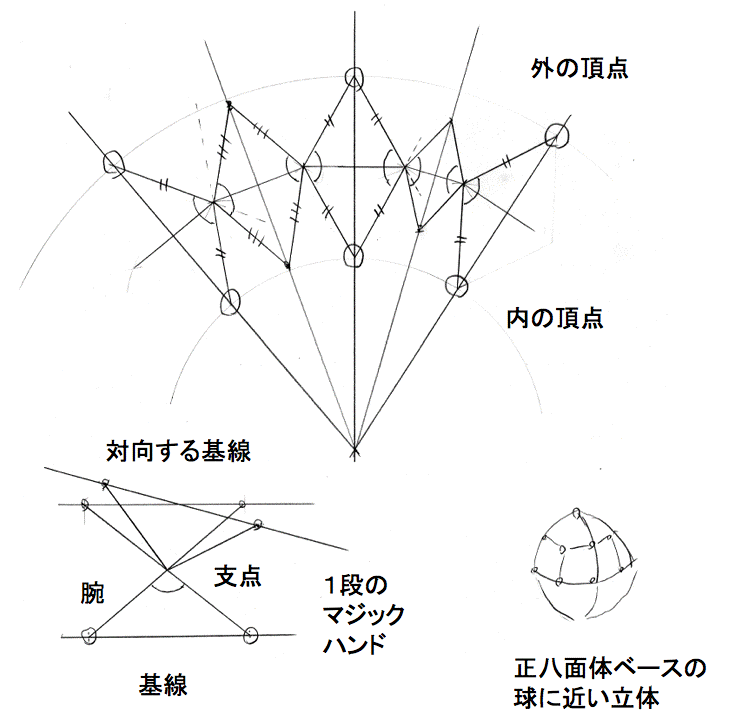
ここで、マジックハンドについて少し呼び方などを定義しておきます。私は全く素人なのでいいかげんな呼び方をしますが、ここでは、上図(左下)のように支点、腕(アーム)、基線、対向する基線と呼ぶことにします。支点の数でマジックハンドの段数を定義します。また、2つの腕が成す角度を腕の広がり角と呼ぶ事にします。普通は腕は真っすぐで、基線と対向する基線は平行を保ったままで、腕の広がり角が小さくなるとともに、基線と対向する基線の距離が広がります。
さて、多面体の頂点をつなぐ場合、基線と対向する基線は一定の角度を保ったまま動かなければなりません。そのためには、支点のところで腕を一定角度で折り曲げれば良いことが分かります。腕の長さを変えるというアイデアもありますが、その場合は、基線と対向基線の成す角度が腕の広がり角に依存してしまうのでうまくいきません。
Mini sphere型の場合は、正多面体ではないので、中心に対して頂点と頂点が成す角が1種類ではありません。すなわち、頂点間の距離も1種類ではありません。しかし、マジックハンドの腕の広がり角は全て同じになるようにしておかなければなりません。なぜならば、支点と基線の間の距離は、腕の広がり角の三角関数(線形でない)で表されるので、もし全ての角度が同じでなければ、マジックハンドの伸び具合が異なってしまって破綻を来すことになります。さて、そうすると、頂点間の距離の違いをどこで調整するかというと、図のように2段にして、間の腕の長さで調整すれば良いわけです。
Hoberman、Sphereの方はさらに多段のマジックハンドを使ったもののようです。いずれにしても、ここで述べた考え方で設計すれば、どんな多面体の頂点でもマジックハンドで簡単につなげそうです。
これは、立方体の頂点が折れ曲がるようになっていると、2通りの正四面体ベースの形(メタン分子のような形)の間で、行ったり来たり変形できるというのが基本的な原理です。
スイッチピッチは、この立方体の辺に当たる部分の真ん中にそれぞれ柱を立てて、そこに球面を張って裏っ返るるようにしようという凄い発想によるものです。具体的には、球面を考えて、形が変わった時の球面がどこで交差するかを考えることによって設計することができます。もし、球面が交わるところで面を切ってしまうことにすると、(最初の写真の)オレンジの凹みの部分とそれと対象な青の小さな3角しか残らないことになります。しかし、凹みの部分の内側は、片方は切って、片方は伸ばすように重ねることができるので、それと対象に外側も頂点を囲むように伸ばすことができます。こうして、凹みの部分以外はほぼ球面になって、裏っ返すことができる形が設計できます。凹みの内側の重なり、あるいは頂点を囲む羽根をどちらに伸ばすか2通りありますので、頂点の回りが右回りと左回りの2通りのスイッチピッチが考えられます。
このスイッチピッチは着想が凄いだけでなく、工学的にも非常に良くできています。宙に浮いて少し遠心力が働くと中間の形になって、そのまま慣性で反対の形に移行して降りてきます。また、内側に入った羽根の部分は内側の頂点を中に押し込む働きもしています。